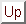Parallelism

The most obvious way to parallelize the minimax algorithm is to divide the search tree and spread it out across several processors. An easy way to do this is to separate the tree at the top level and have each processor investigate a single move. However, if alpha-beta cutoffs are to be used, each tree will have to search for it's own bounds, and can't make use of better bounds found by other processors.

I decided to attempt parallelism using a master and slave paradigm, providing one processor with the bulk of the computation to distribute. Keeping in mind the Younger Brother Wait Concept (Feldman, Mysliwietz, and Monien, 199-), I realized that in order to provide initial alpha-beta cutoff bounds the slaves, the master must fully evaluate the left-most leaf of the tree before distributing any work. Aside from keeping the master primarily idle, the slaves achieve a much better balance of work. I constructed the master to supervise the behavior of the slaves beyond the exploration of the first leaf. Once the slaves are sent a branch of the tree to search, they perform the regular minimax algorithm. This method of breaking up the tree is called Principle Variation Splitting (Marsland, Olafsson, and Schaeffer, 1986).

The two tree division methods just discussed are illustrated in Figure 7.

 
Figure 7: Methods for Splitting a Tree among Processors

Basic parallel algorithm

The master is the processor that starts the game and maintains all of the necessary information throughout. The only section of the game that is parallelized is the minimax function called by the master. Inside this function, the master requests a number of slaves and then proceeds with the minimax function. The slave identification information is stored in an array which the master can search to find idle slaves.

Because bounds are necessary, as discussed later on, the master fully explores the leftmost branch of the tree before distributing any work to slaves. At this point, the master assumes that all of the slaves are inactive. When distribution begins, the master sends a message to each of them, marking them active. When a slave returns, the master processes returned information, marks the slaves as idle and then prepares to redistribute work if there is any.

After all of the moves have been evaluated and all of the messages received by the master, the best score and move are returned and the slaves are removed.

Pseudocode for parallel algorithm

Master:

Parallel_minimax(
begin
    start_slaves(slave_num);
    :
  /*  normal minimax  */
    :
    moves_list = generate_moves(game);
    while (i = 1 to moves_list.length) do 
        if (i = 1)
            /*  master evaluates move using normal minimax calls  */
        else 
            for (j = 1 to slave_num) do
                send_game(slave_num, moves_list[i]);
                moves_list.length = moves_list.length + 1;
            enddo
            for (j = 1 to slave_num) do
                receive_game(slave_num);
                process_results(slave_message);
            enddo
        endif
    enddo
    :
    end_slaves(slave_num);
end.

Slave:

Slave_management()
begin
    while (active) do
        receive_message(message);
        if (game_message) then 
            receive_game(master_message);
            slave_minimax(game information);
            send_results(master, score);
        else
            active = false;
        endif
    enddo
end.

Implementing cutoffs

Since the slaves call the original minimax function, they only need to be switched on to allow cutoffs on their search trees. In order to maximize cutoffs slaves must be provided with with the most current bounds available. To do this, the master communicates with the slaves while they are in the midst of searching their own trees. When a slave returns with bounds that are better than the current bounds held by the master, the master broadcasts these new bounds to the slaves. Slaves check for these new bounds at the beginning of each iteration of minimax, adjusting their behavior as necessary.

Because of the structure of my program, the master never has previous bounds to violate and therefore never cuts off the slaves. However, in a more general algorithm, when the master is searching parts of the tree itself, or when slaves are working for other slaves, it will be necessary to terminate slaves should a cutoff occur.

Pseudocode for Slave minimax with updated bounds management

Slave\_minimax (game information)
begin
        :
        receive_message(new_bounds);
        if (bounds <> better(bounds, new_bounds)) then	
            bounds = new_bounds;
        endif
        minimax (game information);
        :
end.